Z-Scores (part one) (Jump to: Lecture | Video )

Take this example: For the past two years, Joe has been in a bowling league.

First Year Stats:

League Average = 181

Standard Deviation = 12

Joe’s Score in Final Game = 187

Second Year Stats:

League Average = 182

Standard Deviation = 5

Joe’s Score in Final Game = 185

Compared to the rest of the league, in which year was Joe’s score in the final game better?

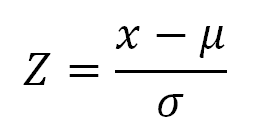
Figure 1.

We can calculate a z-score for each year:

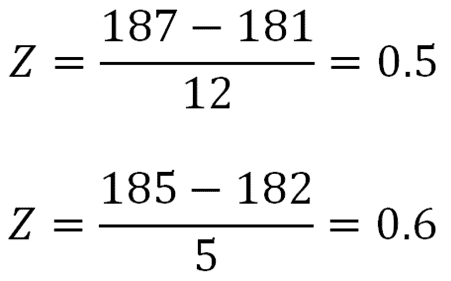
Figure 2.

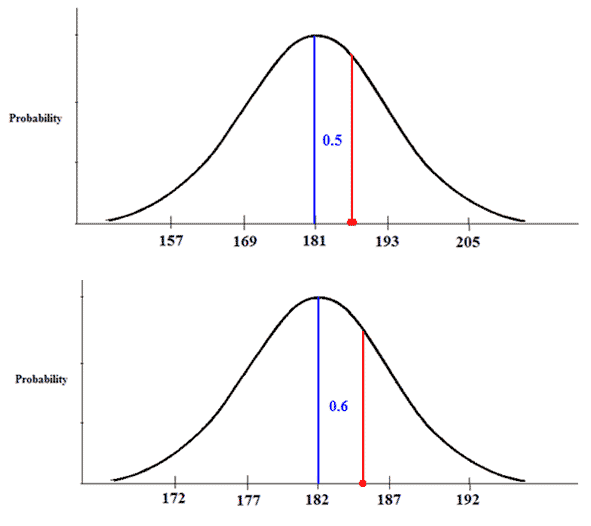
We can then plot the z-scores and compare their placement on the distribution. From the graphs below you can see that compared to the rest of the league, Joe had a better score in his second year.

Figure 3.