Inverse Variation

Navigation

Resources

Direct Variation
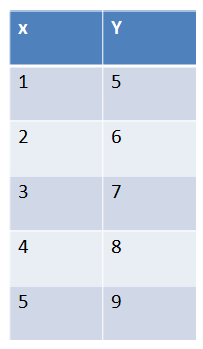
When a value "y" increases as a value "x" increases, direct variation is said to be present.

Below, "x" and "y" vary directly. As one increases, the other increases.

Figure 1.

Inverse Variation
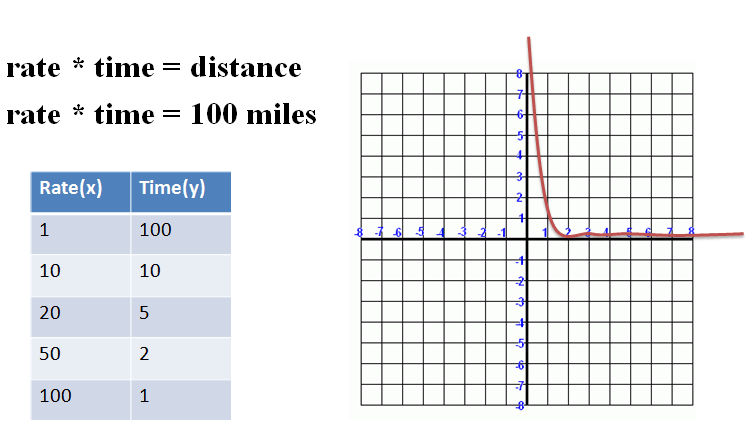
"y" varies inversely with "x" if there is a nonzero constant such that xy = k.

Here, "rate" and "time" vary inversely at a constant rate. As one increases, the other decreases:

Figure 2.