Independent Samples t-Test (Jump to: Lecture | Video )

Let's perform an independent samples t-test: A statistics teacher wants to compare his two classes to see if they performed any differently on the tests he gave that semester. Class A had 25 students with an average score of 70, standard deviation 15. Class B had 20 students with an average score of 74, standard deviation 25. Using alpha 0.05, did these two classes perform differently on the tests?

Steps for Independent Samples t-Test
1. Define Null and Alternative Hypotheses 2. State Alpha 3. Calculate Degrees of Freedom 4. State Decision Rule 5. Calculate Test Statistic 6. State Results 7. State Conclusion

Let's begin.

1. Define Null and Alternative Hypotheses

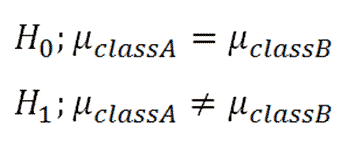
Figure 1.

2. State Alpha

Alpha = 0.05

3. Calculate Degrees of Freedom

Figure 2.

4. State Decision Rule

Using an alpha of 0.05 with a two-tailed test with 43 degrees of freedom, we would expect our distribution to look something like this:

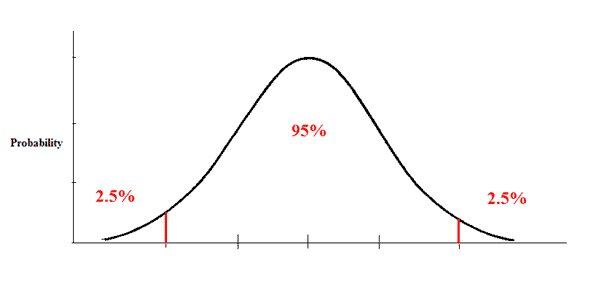
Figure 3.

Use the t-table to look up a two-tailed test with 43 degrees of freedom and an alpha of 0.05. We find a critical value of 2.0167. Thus, our decision rule for this two-tailed test is:

If t is less than -2.0167, or greater than 2.0167, reject the null hypothesis.

5. Calculate Test Statistic

The first step is to calculate the df and SS for each sample:

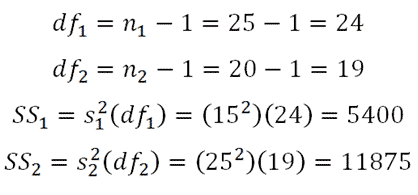
Figure 4.

We then use that information to calculate the pooled variance:

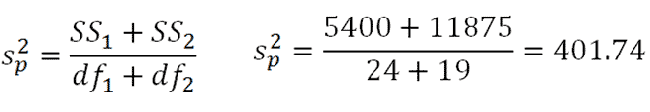
Figure 5.

Finally, we can calculate our t value:

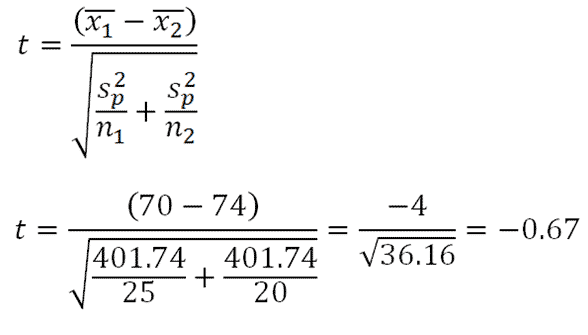
Figure 6.

6. State Results

t = -0.67

Result: Do not reject the null hypothesis.

7. State Conclusion

There was no significant difference between the test performances of Class A and Class B, t = -0.67, p > 0.05.

---